两年前,当Nathan Klein开始他的研究生学业时,他的导师们提出了一个“谦虚的”计划:一起研究理论计算机科学中最著名的难题之一。
即使没有想到可以真的解决它,导师们也认为,Klein会在这个过程中学到很多东西。他接受了这个提议。“我都不知道自己应该被吓倒。”他说,“我只是个博一的研究生——我不知道发生了什么。”
现在,Klein和他在美国华盛顿大学的导师Anna Karlin,Shayan Oveis Gharan于7月在线发表了一篇论文,实现了计算机科学家近半个世纪以来追求的目标:找到了一种更好的方法来解决“旅行推销员”问题的近似方案。
旅行推销员问题(Traveling Salesman Problem)是数学领域的著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
这个组合优化问题,致力于寻求最短(或最“便宜”)的多城市间往返路径距离,其应用范围上至DNA测序,下至乘车物流。几十年来,它促进推动了计算机科学中许多最基本的进步,帮助阐明了线性编程等技术的力量。但研究人员还没有将其可能性探索完全——这并不是因为他们不想尝试。
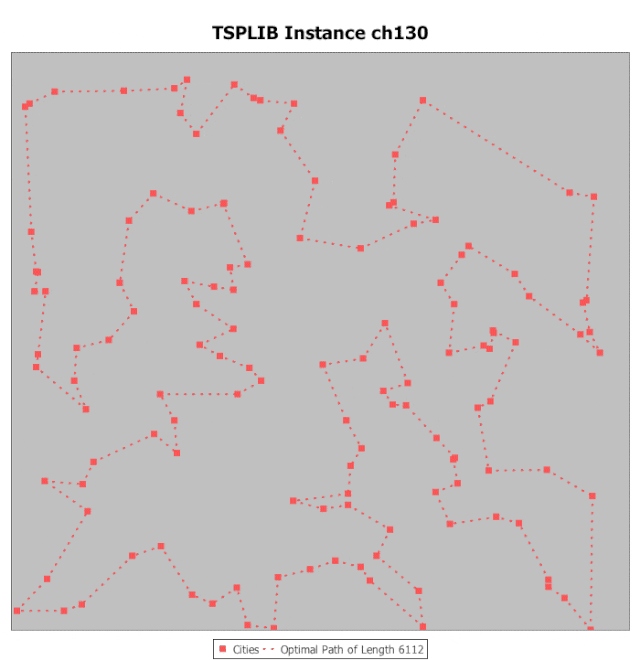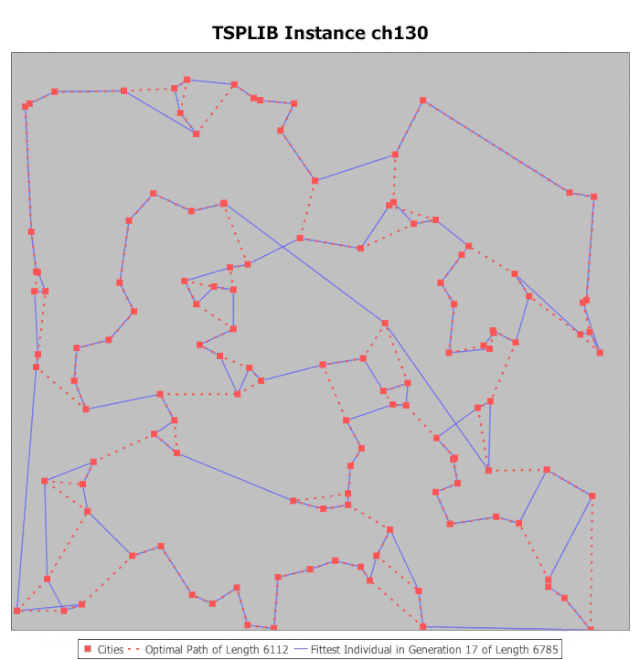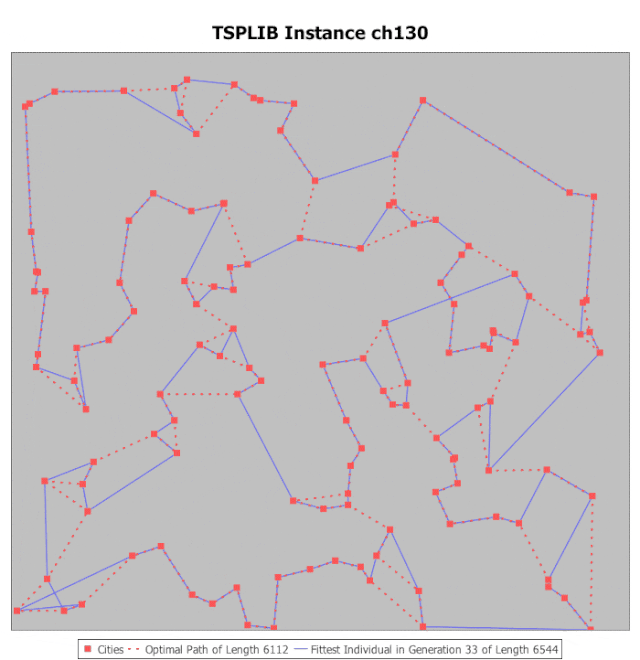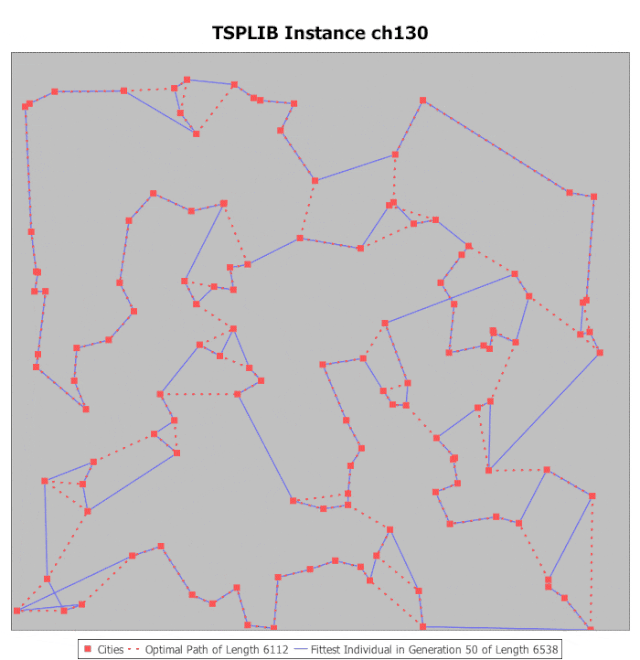
旅行推销员问题。 (图片来源:Gfycat)
正如计算复杂性领域的顶尖专家Christos Papadimitriou喜欢说的那样,旅行推销员问题“不是问题,而是一种瘾”。
多数学者认为,没有一种算法可以有效地从所有可能的城市组合中找出最佳解决方案。但在1976年,Nicos Christofides提出了一种算法,可以高效地找到近似解,令往返距离可以不超出最佳路径的1.5倍。当时,学界期望很快就会有人对Christofides 的简单算法进行改进,并向真正的解决方案进一步接近。但预期的进展并没有到来。

Nicos Christofides
斯坦福大学的 Amin Saberi 说:“很多人花了无数时间,试图改进这个结果。”
现在,Karlin、Klein和Oveis Gharan已经证明,十年前被设计出的一种算法超越了Christofides的算法。虽然新方法只比后者缩短了五千万亿分之一,但这个看似微不足道的进步既突破了理论上的困局,也突破了心理上的。研究人员希望,这将为进一步的改进打开一扇闸门。
“这是我穷尽一生想追求的结果。”康奈尔大学的David Williamson说,他从上世纪80年代起就开始研究旅行推销员问题。
旅行推销员问题作为少数几个被理论计算机科学家经久不息研究的基础性问题之一,被一次又一次地用来测试高效计算的极限。Williamson说,新的结果“是表明高效计算的前沿进展实际上比我们想象得更出色的第一步”。
一个“小”进步
虽然总能找到最短路径的有效方法或许不存在,但我们有可能找到几乎一样好的东西:连接所有城市的最短“树”,也就是不包含闭环的连接(“边”)构成的网络。Christofides的算法使用了这类树作为骨干,增加额外的边,将其转换为往返路径。
任何一条往返路径都必须有偶数数量的边进入每个城市(节点),因为每个到达城市后面都紧跟一个作为出发点的城市。事实证明,反过来也是如此——如果单一网络中的每个城市都有偶数个连接,那么网络的边一定会形成一条往返路径。
连接所有城市的最短树缺乏这种均匀属性,因为任何一个分支末端的城市与另一个城市只有一条边相互连接。因此,为了将最短树变成往返路径,Christofides(已于2019年去世)找到了连接具有奇数边的城市对的最佳方法。然后,他证明了由此产生的往返路径绝不会比可能的最佳往返路径长50%以上。
在这个过程中,他设计了可能是理论计算机科学中最著名的近似算法——它总是教科书和课堂上第一个出现的算法例子。
“每个人都知道这个简单的算法,”法国格勒诺布尔-阿尔卑斯大学和国家科学研究中心的研究员Alantha Newman说,当你认识它的时候,“你知道的已经是当下最先进的知识了。”至少,在今年7月之前,这是事实。
计算机科学家一直怀疑,应该存在一种近似算法能胜过Christofides的算法。毕竟,他简单直观的算法在设计旅行推销员路线时并不总是那么有效,因为连接城市的最短树可能不是你能选择的最佳骨干。例如,假若这棵树有很多分支,分支末端的每个城市都需要与另一个城市进行匹配以形成往返路径,可能会带来很多高成本的新连接。
2010年,佐治亚理工学院的Oveis Gharan、Saberi和Mohit Singh开始琢磨能否改进Christofides的算法:不是选择连接所有城市的最短树,而是从被精心挑选出的集合中随机选择一棵树。他们从旅行推销员问题的另一个版本中获得灵感,在这个问题中,你被允许沿着组合路径旅行——也许你去往丹佛的路线可以分成两段:从芝加哥到丹佛的3/4加上从洛杉矶到丹佛的1/4。
与普通的旅行推销员问题不同,这个分段问题是可以被有效解决的。而且虽然分段路线没有物理意义,但计算机科学家一直认为,最佳的分段路线应该可以为好的普通路线提供大致的轮廓指导。
因此,为了创建他们的算法,Oveis Gharan、Saberi和Singh定义了一个随机过程,该过程挑选出一棵连接所有城市的树,使给定边位于树上的概率等于该边长度在最佳分段路线中的占比。这样的随机过程有很多,所以研究人员选择了一个倾向于产生许多均匀连接城市的树的随机过程。在这个随机过程产出一棵特定的树后,他们的算法将其插入Christofides的方案中,用于匹配具有奇数边的城市,将其转换为往返路径。
不仅在三位研究人员眼中,在其他计算机科学家看来,这种方法似乎都很有前途。“直觉上,它很单纯;”瑞士洛桑联邦理工学院的Ola Svensson说,但“要把它证明出来可就完全不一样了”。
第二年,Oveis Gharan、Saberi和Singh成功地证明了他们的算法在“图形化”旅行推销员问题上胜过Christofides的算法——城市之间的距离由一个网络(不一定包括所有的连接)来表示,在这个网络中,每条边都有相同的长度。但研究人员无法将他们的结果扩展到一般性的旅行推销员问题上:在这个问题上,一些边可能比其他边长很多。
“如果我们必须为这种组合增加一条超级浪费距离的边,那么我们基本上就完蛋了。”Karlin说。
推动边界
尽管如此,Oveis Gharan 还是从那次合作中获得一个不可动摇的信念,那就是他们的算法应该可以在广义旅行推销员问题上击败Christofides 的。“我从来没有怀疑过这一点。”他说。
在之后的岁月里,Oveis Gharan不断在脑海中反刍这个问题。他怀疑,在理论计算机科学界鲜为人知的一门名为“多项式几何”的数学学科中,或许有他需要的工具。因此,当两年前Karlin来找他,建议他们共同指导一个名叫Nathan Klein的优秀新研究生(他主修双专业:数学和大提琴)时,他说:“好吧,让我们试试,我这儿有个好玩的问题。”

左起:Nathan Klein、他的导师Anna Karlin和Shayan Oveis Gharan. (图片来源:Quanta magazine)
Karlin认为,即使没有其他原因,这个课题也是可以让人了解更多多项式几何的有趣机会。“我真的没想到我们能解决这个问题。”她说。
她和Oveis Gharan毫不犹豫地把Klein扔进了计算机科学研究的最深层。Oveis Gharan自己也曾在十年前以研究生身份琢磨了旅行推销员问题一番。而两位导师也一致认同给研究生分配难题的好处,尤其是在头几年,因为他们将不会面对必须取得成果的压力。
三人进入了紧张的合作中。“两年来,这个问题成了我脑海中的一切。”Klein说。
他们把第一年的时间用来解决问题的简化版,以了解所面临的挑战。但即使在完成了这些工作之后,一般性的原问题仍然让他们感觉像是在“完成登月计划”,Klein说。
不过,他们还是用自己的工具找到了思路,尤其是多项式几何。多项式是由数字和指数型变量组成的项的组合(如3x2y+8xz7)。为了研究旅行推销员问题,研究人员将一张城市地图提炼成一个多项式,城市之间的每条边都由一个变量代表,每棵可以连接所有城市的树都由多项式中的一项代表。然后,数值因子对这些项进行加权,以反映每条边在旅行推销员问题的分数解中的价值。
他们发现,这个多项式有一个令人垂涎的特性——“实部稳定性”(real stabilty),这意味着使多项式结果为零的复数部分永远不会位于复平面的上半部分。这个特性的好处是,即使对多项式进行多种改变,它也会保持有效。因此,举例来说,如果研究人员想关注特定城市,他们可以用一个单一变量来代表所有通往城市的不同边,并将代表他们不关心的边的变量设置为1。当他们对这些简化的多项式进行操作时,他们的操作结果仍然具有实部稳定性,这为种种技术打开了大门。
这种方法使得研究人员能够掌握一些问题,如“算法曾多少次被迫连接两个遥远城市”。在一份近80页的分析中,他们成功地证明了该算法在广义旅行推销员问题上胜过了Christofides的算法(该论文还没有经过同行评审,但专家们确信它是正确的)。论文完成后,Oveis Gharan就给他曾经的博导Saberi发了一封邮件。“我想我终于可以毕业了。”他玩笑式地说。
虽然研究人员建立的改进是微乎其微的,但计算机科学家们希望这一突破能进一步激励该领域的快速进展。早在2011年,当Oveis Gharan、Saberi和Singh弄清图形化案例时,就发生过这样的事情。在一年之内,其他研究人员提出了完全不同的算法,极大地改善了上述图形化案例中的近似系数,现在已经降低到40%,而不是 Christofides的50%。
“当他们宣布关于图形化案例的结果时,……让我们认为这是可能的。这鼓舞了我们。”在该案例中取得进一步进展的研究人员之一Svensson说。他多年来一直在尝试击败Christofides的一般性旅行推销员问题的算法。“现在,既然我知道这是可能的,我会再试一次。”他说。
几十年来,已经出现了许多突出的,用于解决旅行推销员问题的新方法。Oveis Gharan希望多项式几何将在舞台上发光发热。
他已经成为了这个工具的热心传播者。在他开始学习这种方法后的十几年里,该方法帮助他证明了各种各样的定理。他说,这个工具“塑造了我的整个职业生涯”。
Newman说,新的旅行推销员问题的结果凸显了这种方法的力量。“这肯定是一种启发,让我们得以去更仔细地观察它。”
Klein现在要找一个新的问题来沉迷了。“失去这个问题让我有点难过,因为它刚刚在我的脑海中建立了那么多结构,现在它们都有点消失了。”他说,但他已经获得了一个最完美的计算机科学研究入门了,“我觉得我们把未知事物的边界向外推动了一点”。